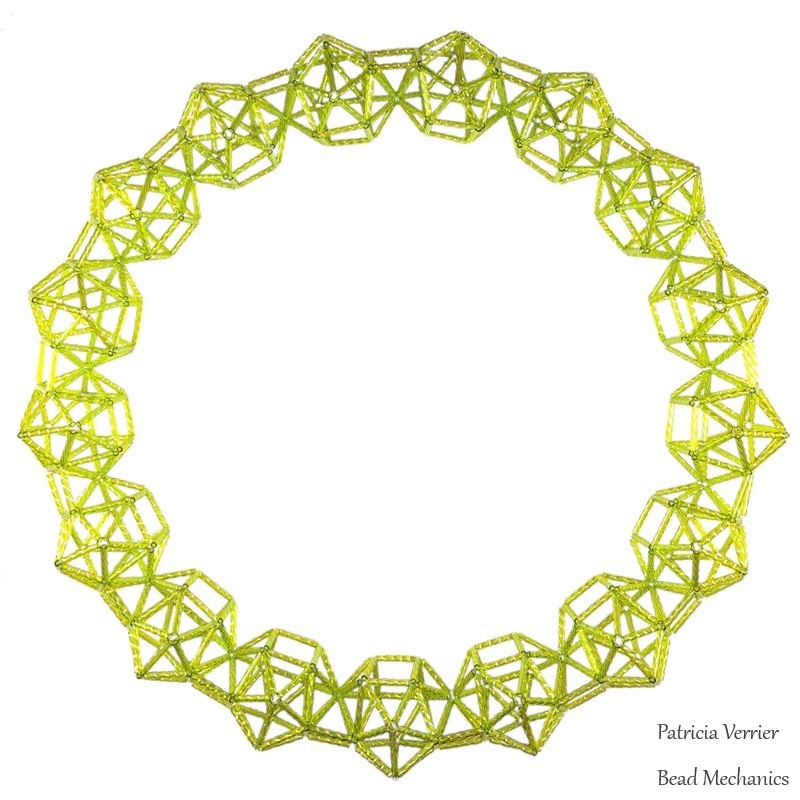
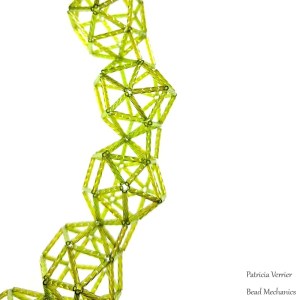
One of the stitches I use a lot for geometric shapes is polyhedral weave – this is like right angle weave, but used to make the various polygons that make up the faces of a polyhedron. It works well with both bugle beads and round beads, and I’ve made a variety of shapes over the years – including some near-miss Johnson Solids and some more complex shapes. However, I’ve never systematically made each one of the Platonic and Archimedean Solids, so I started a study of each using 4mm crackle glass beads and 0.25mm nylon monofilament.

Here are the results for the Platonic solids!

The first and smallest is the tetrahedron. Because of the round beads it doesn’t first look like a tetrahedron – but if you consider that each bead is one edge of the shape you can see the structure underneath. I was a bit concerned that it wouldn’t be possible to weave in the thread on this one, as there isn’t much space, but it actually turned out fine. Even though it’s a simple shape I really like it, and will definitely be using it as a component in other work in the future!

The next two shapes are duals of each other – the octahedron and the cube. If you connect the central point of each face of an octahedron you end up with a cube – a vice versa. The beaded versions of these two shapes therefore look very similar when made with round beads, as you can see in the photo below. The one on the left is an octahedron and the one on the right is a cube – the only difference is the direction the thread goes – otherwise they look almost identical! Made this way the cube is just a standard cubic right angle weave unit, while the octahedron is different thread path – which opens up some interesting design options for combining shapes in larger designs.

The last two shapes are also duals of each other – the icosahedron (left) and the dodecahedron (right). I’ve made many of these polyhedral RAW dodecahedrons over the years, but I don’t think I’ve ever made an icosahedron. Although they are essentially the same shape overall when made this way, I think the different orientation of the beads in the icosahedron make it a little bit more interesting.

This was a very simple study of the five Platonic solids, but has provided several design ideas. The next task is the Archimedean solids!

The last in the series of polyhedra rings is a ring of 17 Disphenocingulum:

A Disphenocingulum is Johnson Solid J90, as is made up of 4 squares and 20 triangles. It’s sets of triangular pyramids joined together with pairs of squares:

It’s not the easiest shape to make, as it’s easy to lose track of the triangles, but it got easier after 17 of them! It’s made with polyhedral angle weave, 12mm bugle beads and nylon monofilament like the others in the series.

The disphenocingulum are joined together square pyramids on the outside of the ring, with the base of the pyramid linking up with a pair of the squares on the J90s to make a ribbon of squares all around the edge.

Like most of this series, I learnt about this shape on Rafael Millán’s GeoMag website. It’s much larger than the other three in this series, and unfortunately it’s not very stable at all. The disphenocingulum themselves tend to collapse at the slightest touch, and generally look a little bit warped. This means the ring is not very stable as well, as the polyhedra need to be exactly in the right position to keep it in shape.

This was the last in a series of rings of polyhedra – here are all four together:

From left to right it’s a ring of 14 snub disphenoids (J84), a ring of 15 hebesphenomegacoronona (J89), a ring of 16 sphenocoronae (J86) and this ring of 17 disphenocingulum (J90). This was a fun series to make, and I think I’ll try and hang them on a wall somewhere they will catch the light, as I love how the rainbow finish twisted bugle beads sparkle in the sun!

Next in the series of bugle bead rings of polyhedra is a ring of 16 Sphenocoronae!

A Sphenocoronae is another Johnson Solid – this time J86. It’s made up of 12 triangles and 2 squares. It’s essentially two pentagonal pyramids on a base of 2 squares, with 2 more triangles filling in the gaps:

It’s quite a nice shape to weave together, and like the previous two rings this one is made with 12mm bugles, nylon monofilament and polyhedral angle weave. It does use an extra “linking” bugle to join the polyhedra together – forming a tetrahedra in between each sphenocoronae on the outside of the ring.

Like the ring of snub disphenoids, I learnt about this shape on Rafael Millán’s GeoMag website.

This one is quite a bit larger than the other two, so doesn’t work as a bangle with 12mm beads. I’m enjoying making this series though and have one more shape to try!